如何解决无尽的拉格朗日飞机装载中的难题
来源:五宝网
发布时间:2023-11-20 15:09:01
飞机装载是无尽的拉格朗日中提升战斗力的关键环节,但很多小伙伴在实际操作中会遇到各种问题。首先需要明确的是,飞机装载并非简单地把装备塞进机库,而是要根据飞机类型、战斗定位和敌方阵容进行针对性搭配。比如战斗机适合携带高爆发武器,而轰炸机则需要优先考虑生存能力。每种飞机的属性面板都会明确标注可搭载的装备类型,仔细阅读这些信息能避免很多无效操作。
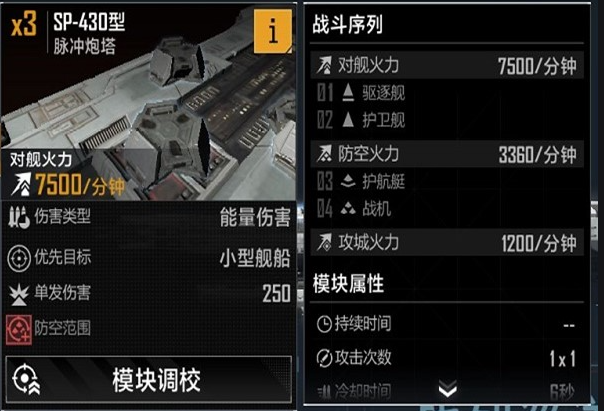
合理分配装备资源是解决装载难题的核心思路。游戏中的装备分为武器、防护、引擎和其他四类,每类装备都有独特的属性和效果。武器类决定输出能力,防护类提升生存能力,引擎类影响机动性,其他类则提供特殊功能。建议优先根据飞机的战斗角色选择主属性,比如对空型飞机重点强化命中率和闪避,对舰型飞机则优先提升攻城伤害。不要盲目追求高等级装备,低等级但属性契合的装备往往比高等级但不匹配的装备更实用。
实战演练是检验装载方案的最佳方式。游戏提供了丰富的战斗场景,可以通过反复测试不同装备组合的效果来优化配置。注意观察战斗回放中飞机的表现,比如输出是否达标、生存时间是否合理、特殊技能是否有效触发等。这些细节能帮助调整装备搭配,比如发现飞机经常被秒杀就需要增加防护装备,输出不足则要考虑更换武器类型。实战中也要灵活调整,比如面对高防御敌人时可以临时更换穿透型武器。
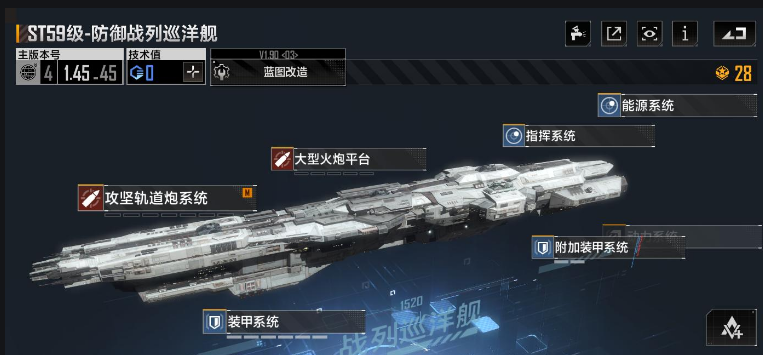
蓝图系统可以保存成功的装载方案,方便快速切换;研究树能解锁更高级的装载选项;联盟中的大佬们也经常分享实用的装载技巧。多和其他玩家交流能少走很多弯路,毕竟这游戏的飞机搭配千变万化,一个人的经验终究有限。只要耐心尝试和调整,总能找到适合自己的解决方案。
相关资讯
+More
最新资讯
+More
热门攻略
+More
03-06
雄远镖局在卧虎藏龙中扮演的是什么角色
雄远镖局在卧虎藏龙的故事中,首先是主角俞秀莲的身份根基与事业...
-
03-06
-
03-05
-
03-05
-
03-05
-
03-05
03-05
明日之后赠送哪些东西亲密度会比较高
赠送特定物品是快速提升与好友或NPC亲密度的重要途径。提升亲...
-
03-04
-
03-06
-
03-05
-
03-05
-
03-05